Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
The atmospheric boundary layer is important for the global climate system by providing a boundary condition for the interior flows. Its extreme parameter regime, e.g., the huge Reynold number that is currently impossible to achieve in numerical simulations and laboratory experiments, brings about great challenges to our geophysics and fluid communities, particularly, how to fill the gap between phenomenological models and first principle (Navier-Stokes equations). Furthermore, the complex nature of the atmospheric boundary layer underscores the need for robust theoretical understanding and expressions that can withstand different scenarios, such as sand-containing flow. These perspectives mentioned above highlight the importance of our theoretical work in providing a solid foundation for practical applications.
Townsend’s attached eddy hypothesis (AEH), a foundation of many turbulence modelling, gives a phenomenological description of the flow kinematics in the logarithmic layer, but it suffers from two major weaknesses. First, AEH does not predict the constants in its velocity scalings, and second, none of the predicted velocity scalings can be obtained from the Navier-Stokes (NS) equations under AEH’s assumptions. These two weaknesses separate AEH from more credible theories like Kolmogorov’s theory of homogeneous isotropic turbulence, which, despite its phenomenological nature, has one velocity scaling that can be derived from the NS equation. From the K´arm´an-HowarthMonin equation, which is derived from the NS equation, we asymptotically obtain the balance between the divergence of the third-order structure function vector and the shear production, which leads to the AEH predicted logarithmic dependence of the longitudinal third-order structure function with determined coefficients [Xie et al., 2021, Phys. Rev. Fluids]. This work confirms the consistency between the first principle (NS equation) and the phenomenological description (AEH). Also, by assuming self-similarity, the matching procedure for the second-order structure function provides a relation between the Kolmogorov constant, the K´arm´an constant and the Townsend-Perry constant, indicating two independent parameters out of the three.
Making use of the atmospheric boundary layer (ASL) turbulence with extremely high friction Reynolds numbers up to O(10^7), which is unreachable by current numerical simulations and laboratory experiments, we justified the balance in the KHM equation and the structure-function expressions using data measured from the Qingtu Lake Observation Array; also the speciality of the measured data from natural flow enabled us to check the robustness of these relations in clear-air and sand-containing scenarios (cf. left panel of the figure below [Zhang et al., 2022, Phys. Rev. Fluids]).
In addition, we constructed a statistical autoregressive moving average model consisting of the history and random effects for the streamwise velocity fluctuation in boundary-layer turbulence. By proposing a dynamical attached-eddy perspective, this model provides a global analytical expression for the second-order structure function covering the inertial, dynamic and large-scale ranges [Zhang et al., 2024, J. Fluid Mech.]. A consequent double-log expression for the characteristic length scale, which corrects the empirical logarithmic expression, is derived and is robust by its applicability even when the statistics of ASL deviate from those of canonical boundary-layer turbulence (right panel of the figure below). Thus, the autoregressive moving average model is practical for analysing and generating ASL turbulent time series.
(Work with Fei-Chi Zhang, Prof. Song Xi Chen and Prof. Xiaojiang Zheng.)
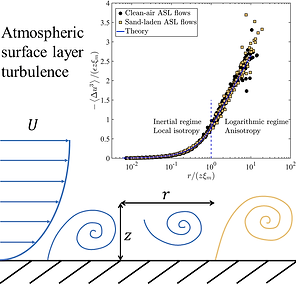
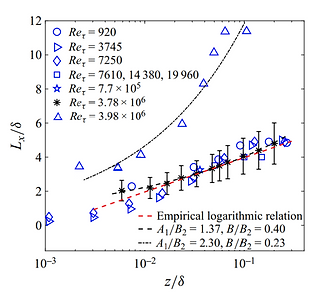
Figure: Left: Illustration of boundary-layer turbulence and the theoretical expression that describes atmospheric data with and without sand. Right: Theoretical expressions capture atmospheric characteristic scales under complicated environmental conditions.