Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Linearly unstable fluid systems are ubiquitous, and they approach (statistically) steady states due to nonlinear effects. I study the saturation of unstable perturbations in three systems: (i) magnetorotational instability, (ii) salt fingering convection and (iii) equatorial convection.
Magnetorotational instability
The magnetorotational instability is widely believed to be responsible for outward angular momentum transport in astrophysical accretion disks. The efficiency of this transport depends on the amplitude of this instability in the saturated state. We employ an asymptotic expansion based on an explicit, astrophysically motivated timescale separation between the orbital period, Alfv\'en crossing time and viscous or resistive dissipation timescales, originally proposed by Knobloch and Julien, Phys. Fluids 17, 094106 (2005), to formulate a semi-analytical description of the saturated state in an incompressible disk. In our approach, a Keplerian shear flow is maintained by the central mass but the instability saturates via \rev{the generation of a mean vertical magnetic field}. The theory assumes that the time-averaged angular momentum flux and the radial magnetic flux are constant and determines both self-consistently. The results predict that, depending on parameters, steady saturation may be supercritical or subcritical, and in the latter case that the upper (lower) solution branch is always stable (unstable). The angular momentum flux is always outward, consistent with the presence of accretion, and for fixed wavenumber peaks in the subcritical regime. The limit of infinite Reynolds number at large but finite magnetic Reynolds number is also discussed.
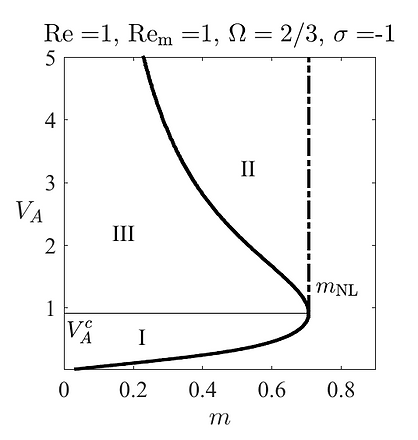
The right figure shows different regimes of saturation. Regime I denotes the supercritical regime containing an unstable trivial state and a stable finite amplitude state. Regime II denotes the subcritical region with three states, the stable trivial state, the upper branch nonlinear states, and the lower branch intermediate unstable nonlinear states. In regime III one finds an unstable trivial state and a stable but disconnected finite amplitude state.
(Work with Prof. Keith Julien and Prof. Edgar Knobloch.)
Salt fingering convection
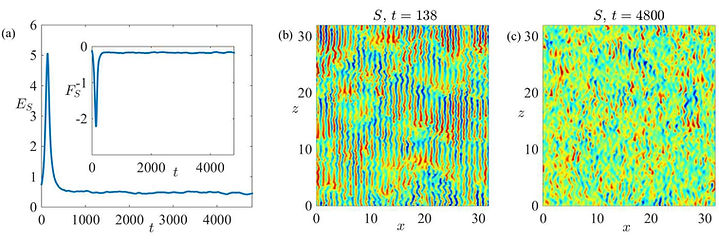
A simple model of nonlinear salt-finger convection in two dimensions is studied, following Radko and Stern (J. Marine Res. 57, 471–502 (1999)). The model is valid in the limit of small solute diffusivity and strong salinity driving and is therefore relevant to both oceanographic and astrophysical applications. For large Prandtl numbers the model takes the form of a prognostic equation coupled to a diagnostic equation. Saturation of the instability occurs via secondary instabilities together with salt-finger collisions. Two distinct regimes are identified characterized by the power-law dependence of the energy and salinity flux on the salinity forcing and their dependence on the domain size is studied. A theoretical understanding of the exponents is developed, closely informed by numerical simulations. These indicate that a third regime, at yet stronger forcing, is likely to be present. The statistically stationary state is characterized in terms of spectra and probability density functions. The figure below shows (a) Evolution of the total energy (main panel) and salinity flux (inset) with time. (b) The finger-dominant state at t = 138. (c) The instantaneous statistically steady state at t = 4800.
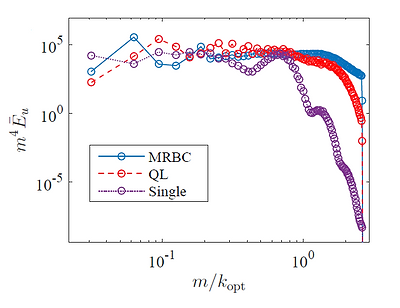
Jet formation is also observed in the two-dimensional salt fingering convection, shown in the figure below on the left. Three hierarchical models, the MRBC and further reductions in the form of quasilinear and single-mode approximations, are used to confirm that jets form and are sustained as a result of the interaction between fluctuations (salt fingers) and large-scale horizontally averaged horizontal flows (jets). Even though the small-scale structures exhibited by the three models exhibit clear differences, all three produce the same power-law spectrum of the mean fields at large vertical scales: in all the spectrum of the jet kinetic energy scales as $m^{-4}$, shown in the bottom right panel.

(Work with Dr. Benjamin Miquel, Prof. Keith Julien and Prof. Edgar Knobloch.)
Equatorial convection
to appear.
(Work with Dr. Benjamin Miquel, Prof. Keith Julien and Prof. Edgar Knobloch.)