Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Isotropic two-dimensional turbulence
We derive and investigate exact expressions for third-order structure functions in stationary isotropic two-dimensional turbulence, assuming a statistical balance between random forcing and dissipation both at small and large scales. Our results extend previously derived asymptotic expressions in the enstrophy and energy inertial ranges by providing uniformly valid expressions that apply across the entire non-dissipative range, which, importantly, includes the forcing scales. In the special case of white noise in time forcing this leads to explicit predictions for the third-order structure functions, which are successfully tested against previously published high-resolution numerical simulations. We also consider spectral energy transfer rates and suggest and test a simple robust diagnostic formula that is useful when forcing is applied at more than one scale.
Figure on the right shows the comparison of predicted structure function (blue curve) with the data from Figure 3 of Boffetta & Musacchio (2010) (red circles), where the associated high-resolution numerical simulation (run E) used 327682^2 grid points. The axis labels have been chosen for easy comparison with Boffetta & Musacchio (2010). The horizontal dashed lines mark the constant 3/2, the inset enlarges the rectangular transition region, and kf = 1/lf .
(Work with Prof. Oliver Bühler.)

Departure from statistical equilibrium of large-scale turbulent dynamics
Understanding turbulence, the last and great unsolved problem of classical physics, from the perspective of statistical physics is promising and fascinating. Numerical and experimental researches show that large-scale properties of three-dimensional homogeneous isotropic turbulence can be described to a large degree by the equilibrium statistical mechanics. This work quantified the departure from statistical equilibrium using the odd-part probability density functions (PDFs) of velocity differences at large separations [Ding et al., 2024, J. Fluid Mech.]. Based on the analytical solution of the K´arm´an–Howarth–Monin equation, this work first proved the nonzeroness of the odd-part PDF. With fast decaying external forcing, we also proved a power-function decay of the third-order structure function with a universal exponent of -2, implying a strong large-small scale interaction. Under the assumption that forcing controls the large-scale dynamics, we propose a conjugate regime to classic forcing-independent Kolmogorov’s inertial range. Therefore, the odd-part PDFs of velocity difference at large scales are self-similar, and all the odd-order structure functions have a power-function decay with universal exponent -2, shown in the right figure. This work helps us to obtain a comprehensive understanding of turbulence
(Work with Dr. Mengjie Ding.)
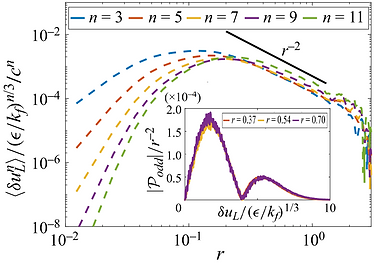
Figure: Universal power-function decay of odd-order structure function with exponent −2. The insetshows the self-similarity of the odd-part of the large-scale velocity difference PDFs.
Bolgiano–Obukhov scaling in two-dimensional Isotropic convection
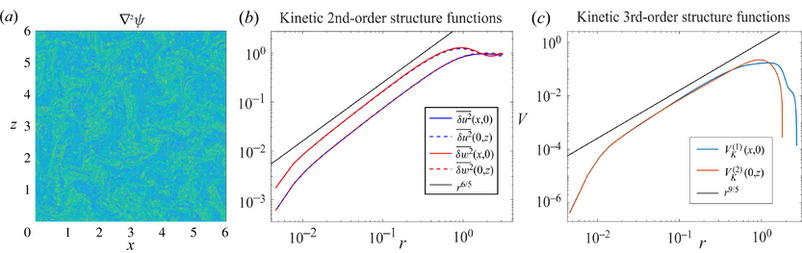
Bolgiano–Obukhov (BO) scaling was initially proposed to describe the scale-dependent statistics in stably stratified turbulence by capturing the effect of potential and kinetic energy interaction. Its existence in Rayleigh–Benard convection (RBC) has long been speculated. However, no conclusive evidence has been found due to the inhomogeneity and anisotropy of the flow and the lack of clear scale separation. This work constructed an idealized isotropic convection system by introducing an additional horizontal buoyancy field to RBC in a doubly periodic domain [Xie and Huang, 2022, J. Fluid Mech.]. Therefore, we theoretically obtained the BO scaling from the K´arm´an–Howarth–Monin equations and checked them using numerical simulations (cf. below figure). These theoretical and numerical results unveil the relation between energy distribution in the scale space and the direction of energy flux in the kinetic and potential energy interaction scenario, which is crucial for natural turbulence.
(Work with Prof. Shi-Di Huang.)
Statistics of velocity circulations in two-dimensional turbulence
Universality is a key topic in turbulence study. Migdal proposed the area rule of velocity circulation around simple loops, stating that when the scale of a loop lies in the inertial range of three-dimensional turbulence, the circulation statistics only depend on the minimum area enclosed by the loop. A natural question is whether the area rule applies to two-dimensional turbulence, which possesses energy and enstrophy inertial ranges. We experimentally studied the velocity circulation in a quasi-two-dimensional turbulent flow and show that the area rule of circulation around simple loops holds in both energy and enstrophy inertial ranges [Zhu et al., 2023, Phys. Rev. Lett.], which are shown in panels (a) and (b) of the figure below. In addition, in the energy inertial range, the circulation is bifractal, which is the same as those in three-dimensional and quantum turbulence, implying the circulation as a simple quantity to explore the turbulence universality (below figure 8(c)).
(Work with Prof. Hang-Yu Zhu and Ke-Qing Xia.)

Figure: (a) and (b) present the area rule of circulation in the enstrophy and energy inertial ranges, respectively. (c) shows the universal bifractal behaviour of two-dimensional,three-dimensional and quantum turbulence using the scaling exponents.