Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Jin-Han Xie's Research
Three main reasons of wave-mean flow interaction in fluid are studied: (1) viscosity effect, which is of special importance in small-scale flows, is studied by two microfluidic problems (see Acoustic streaming and Spherical particle below for detail), (2) the inviscid interaction can be captured by conservation laws, as is shown in the study of Near-inertial wave and mean flow interaction using Hamiltonian fluid mechanics, (3) singularity, which is studied in the Topographic wave and shear mean flow interaction.
Acoustic Streaming
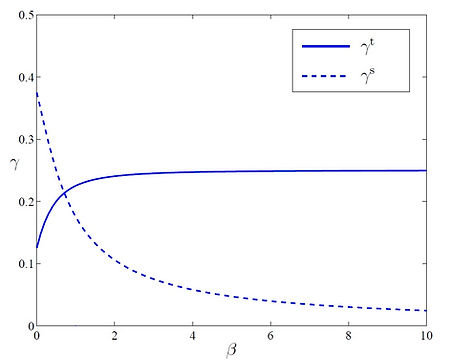
In microfluidic applications involving high-frequency acoustic waves over a solid boundary, the Stokes boundary layer thickness δ is so small that some non-negligible slip may occur at the fluid-solid interface. This paper assesses the impact of this slip by revisiting the classical problem of steady acoustic streaming over a flat boundary, replacing the no-slip boundary condition with the Navier condition u|y=0 = Ls∂yu, where u is the velocity tangent to the boundary y = 0, and the parameter Ls is the slip length. A general expression is obtained for the streaming velocity across the boundary layer as a function of the dimensionless parameter β = Ls/δ. The limit outside the boundary layer provides an effective slip velocity satisfied by the interior mean flow. Particularising to travelling and standing waves shows that the boundary slip respectively increases and decreases the streaming velocity. Details can be found in a paper on this topic.
The figure on the right shows how the standing wave streaming (γs) and travelling wave streaming (γt) modified by parameter β.
(Work with Prof. Jacques Vanneste.)
Spherical particle
A rigid spherical particle in an acoustic wave field oscillates at the wave period but has also a mean motion on a longer time scale. The dynamics of this mean motion is crucial for numerous applications of acoustic microfluidics, including particle manipulation and flow visualisation. It is controlled by four physical effects: acoustic pressure, streaming, inertia and viscous drag. In this research, we carry out a systematic multiscale analysis of the problem in order to assess the relative importance of these effects depending on the parameters of the system that include wave amplitude, wavelength, sound speed, sphere radius, and viscosity. We identify two distinguished regimes characterised by a balance among three of the four effects, and we derive the equations that govern the mean particle motion in each regime. This recovers and organises classical results by King, Gor'kov and Doinikov, clarifies the range of validity of these results, and reveals a new nonlinear dynamical regime. In this regime, the mean motion of the particle remains intimately coupled to that of the surrounding fluid, and while viscosity affects the fluid motion, it plays no part in the acoustic pressure. Simplified equations, valid when only two physical effects control the fluid motion are also derived. They are used to obtain sufficient conditions for the particle to behave as a passive tracer of the Lagrangian mean fluid motion. Details can be found in a paper on this topic.
the figure on the right shows the particle collection in the new regime, the power-law decay instead of exponential decay is discovered.
(Work with Prof. Jacques Vanneste.)

Near-inertial wave
The interactions of near-inertial waves with mesoscale turbulence play a role in the ocean circulation that remains poorly understood. To examine this, we derive a simplified model coupling the Young-Ben Jelloul model of NIW propagation with a quasi-geostrophic model describing mesoscale motion. The model is derived using variational approach combining Whitham averaging, geometric generalised Lagrangian mean theory, and Salmon's flow-map decomposition. Its conservation of potential vorticity, wave action and total energy make it suitable to study the interactions between NIWs and QG motion over long time scales. A correspondent shallow water model is also obtained for its simple numerical cost. The figure on the right displaying the interaction between a NIW packet and unidirectional mean stream: Wave amplitude and change in the mean velocity are shown in the upper and lower row. The downward propagating NIWs induce a mean flow change, which slows down the original mean flow. light (yellow) and dark (red) contours correspond to positive and negative values. Further details can be found in a paper.
(Work with Prof. Jacques Vanneste. I thank Dr. Eric Danioux and Dr. Yue-Kin Tsang for the discussions.)

Topographic wave
The interactions between topographic waves and mean flow in a rotating fluid are concentrated near an inertial level where the Doppler-shifted wave frequency matches the Coriolis frequency. We analyse these interactions in a linear shear flow at small Rossby number, Ro << 1. By applying a combination of Fourier transform, WKB and saddle-point methods we obtain the form of the wave in different regions and derive the quasigeostrophic mean-flow response. The interaction region is concentrated in a thin, O(Ro) region around the inertial level, is located a large distance downstream of the topography and has a large streamwise extent compared with the mountain range by the square root of small Rossby number. This is shown in the figure on the right. Further details can be found in a paper.
(Work with Prof. Jacques Vanneste.)
